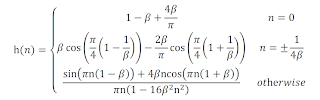modulation BPSK, QPSK,8 QAM,Square Root Raised Cosine (SQRC), and demodulation: May 2013

Wednesday, 29 May 2013

example of simulate code matlab for BPSK, QPSK, 8 QAM, square root raised cosine filter

In this project we are simulating code matlab program three modulation schemes; those are namely BPSK, QPSK and 8-QAM.Firstly, we applied Rectangular pulse shaping (RPS) to BPSK, QPSK and 8 QAM. Secondly,we considered BPSK modulation scheme and simulated the system using Square Root Raised Cosine (SQRC) filter as pulse shaping filter and matched filter and we found minimum number of co-efficientsuch that the loss did not exceed 0.5db .Applied same filter to QPSK and 8-QAM and compared the results.We evaluated the coded performance of BPSK, QPSK and 8QAM with SQRC pulse shaping.Finally, we analyzed the transmitted signal spectrum in each case.

1 INTRODUCTION

In digital communication different types of modulations scheme are used to transfer the data from one place to another. Among these modulation schemes the most common modulation schemes are Binary Phase Shift Keying (BPSK), Quadrature Phase Shift Keying and Quadrature Amplitude Shift Keying (QAM). A brief description of these schemes are as follows.

1.1 Binary phase shift keying (BPSK)

Binary phase shift keying (BPSK) is simplest form of phase shift keying (PSK).It uses two phases which are separated by 180⁰ .And it is also termed as 2-PSK,the Bit Error Rate (BER)of BPSK in AWGN can be calculated as

The constellation diagram of BPSK signal is as follows.

Fig 1.1: Constellation diagram of BPSK

In this bits are converted into antipodal noise symbols. It is unsuitable for high data rate applications because it is only modulate 1bit/symbol. BPSK is functionally equivalent to 2-QAM modulation.

1.2 Quadrature Phase Shift-Keying (QPSK)

In Quadrature Phase Shift Keying (QPSK), there is the phase difference of 90^o between transmitted signals. The transmitted signal can be expressed as

The constellation diagram of QPSK signal is as follows.

Fig 1.2: QPSK constellation diagram

1.3 Quadrature Amplitude Modulation (8 QAM)

In Quadrature Amplitude Modulation (QAM) each signal is transmitted as two components. The components are in-phase and quadrature and these components are 90^o phase from each other.

The bit error rate formula of QAM is.

The organization of this report is as follows:

In section 2, we discussed about the background and simulation model for simulation of BPSK, QPSK and 8 QAM with rectangular, SQRC pulse shaping and Hamming code. In section 3 we discussed the result obtained from the simulation. Finally the conclusion is presented in section 4

2 Bit generation and mapping with SIMULATION MODEL

In this project we developed a general procedure for each modulation. The following block diagram shows the simulation model.

Fig 2.1: Simulation model

The brief description of each simulation block is follows.

2.1 Bit Generation

The Bit Generation block main function is to generate the bit with equal probability.

2.2 Mapping

The main function mapping is to covertthe bitstream into symbols according to each modulation scheme.

For BPSK each zero is mapped to +1 and ones are mapped to -1. In QPSK, the mapper block converts each two bits block into an in phase component and a quadrature component.

Table 2.1:

For QAM we took the blocks of three bits and mapped the bits according to the given gray coding.

2.3 Pulse Shaping Filter

The given Raised cosine filter is

It is implement as SQRC for evaluating the performance of the three modulation schemes.

2.4 Noise

The noise variance is calculated according to Eb/No and in this project we added AWGN noise and it is calculated by multiplying the noise variance with the matrix containing the random number with zero mean and that variance is equal to one. The noise is then added to the transmitted signal to get noisy signal.

2.5 Matched Filter

Now the transmitted signal is noisy signal and it is passed through the matched filter where it samples every T Seconds (For rectangular pulse shaping the sampling time T=1, for SQRC the sampling time T=4)

2.6 Decision

This block recovers the bits from the received samples. This block compares the received point with the thresholds to find the region in which the point lies and then decided the signal. After making the decision it then converts the received signal to the respective bits.

2.7 Comparison

The transmitted bits are compared to the received bits to find the erroneous bits and finally the bit error rate is calculated using the below formula

2.9 Encoder and Decoder

The encoder encodes the each 4-bit block into a 7-bit code word. This code word is fed into the system, at this time the output of the decision block will be the received code word rather than received bits. These code words may contain erroneous bits. The decoder will perform error check by taking 7bit blocks from the received bit stream of code words .It calculates the syndrome of each received code word. This syndrome is used to find the error pattern using syndrome LUT. Finally the corrected code word is generated and the data bits are recovered from each corrected code word.

3 Simulation Results

In this section we will discuss the simulation results of BPSK, QPSK, QAM and the obtained results are compared with theoretical values.

3.1 BPSK and QPSK with Rectangular Pulse Shaping Filter

The performance of BPSK and QPSK system in terms of BER vsEb/No is evaluated in Matlab. Both the QPSK and BPSK has same performance curves. The following figure show the BER curve for the simulated and theoretical system. It can be seen the two curves overlap each other.

Fig3.1: Simulation results of BPSK & QPSK with Rectangular Pulse Shaping

There is no difference between the simulation and the theoretical curves of Eb/N0 vs BER for three modulation schemes .In this context 8QAM provides better performance than BPSK & QPSK .

3.2 8 QAM with Rectangular pulse shaping filter

The communication system with 8 QAM modulation is simulated using the same simulation model as discussed in section 2. Only the function of mapper is changed. The following figure shows the simulated and theoretical curves of 8 QAM system, 8 QAM with pulse rectangular pulse shaping filter

Fig 3.2: 8 QAM with Rectangular Pulse Shaping Filter

3.3 Uncoded Performance of BPSK with SQRC

In this simulation first we applied the SQRC to the BPSK modulation. The SQRC filter is implemented using the FIR filter given the objective of this project. It was found that number of coefficients of the FIR filter affects the performance of the system. We did multiple simulation to find the minimum number of coefficient such that the loss did not exceed 0.5db
at 10^-5 BER. We found these number of coefficients to be 25. The following figure shows the plot of the SQRC with 25 coefficients.

Fig 3.3: Square root raised cosine filter

The performance curve of BPSK system after applying the FIR filter is shown in figure. It can be observed that the loss at BER of 10^-5 is less than 0.5dB.

Fig 3.4: BPSK with SQRC

3.4 Uncoded Performance of QPSK with SQRC

The filter obtained for BPSK simulation is used to evaluate the performance of QPSK. For QPSK system, the lossat BER of 10^-5 is same as BPSK. The following figure shows the performance of QPSK system after applying the SQRC filter.

Fig 3.5: QPSK with SQRC

3.5 8QAM with SQRC

However, the performance of BPSK and QPSK was same after applying the SQRC filter. But when the same filter was applied to the 8 QAM system it was noticed that the loss at BER of 10^-5 exceeded to 1.5dB.

Fig 3.6: 8QAM with SQRC

3.6 Coded Performance of BPSK with SQRC

In BPSK & QPSK coded performance is better than the uncoded performance.The coding gain at 10^-5 is 0.2dB.The coding gain can be increased if we increase the number of coefficients of the FIR filter. Also notice that the difference between the simulation and theoretical curve for coded performance is due to the fact that the formulae used to evaluate the theoretical coded performance is actually an approximation value. \

Fig 3.7: Coded BPSK with SQRC

3.7 Coded Performance of QPSK with SQRC

The coded performance of the QPSK system is same as the BPSK system with coding gain of 0.2dB at BER of 10^-5.

Fig 3.8: Coded QPSK with SQRC

3.8 8 QAM with Code

In QAM the coding gain at 10^-5 is 0dB. We obtained this small value of coding gain because due to the SQRC filter there is loss of 1.5dB on uncoded performance. Hence if we increase the number of coefficient in the FIR filter we can increase the coding gain. The following figure shows the BER performance of 8 QAM when applied with Hamming coding.

Fig 3.9: Coded 8-QAM with SQRC

simulate the hamming code with bit error rate

In this project we simulated BPSK, QPSK and 8 QAM each with Rectangular pulse shaping and Square root raised cosine. Also we applied Hamming code (7,4) and generated the Bit Error Rate (BER) performance graphs. The number of coefficients for the FIR Raised cosine filter was found to be 25.Usiing this filter it was observed that dB loss at BER of 10^-5 was less than0.5dB for BPSK and QPSK and it was exceeded to 1.5dB for 8-QAM.The coded performance was also simulated and found that coding gain was 0.2dB for BPSK/QPSK. Whereas, it was 0dB for QAM at BER of 10^-5.

Tuesday, 28 May 2013

Code MATLAB, Simulated, QPSK, BPSK, 8 QAM, coded, uncoded, SQRC,

simulated

BPSK MATLAB code

clc;

clear all;

bits=1000000;

data=randint(1,bits)>0.5;

ebno=0:10;

BER=zeros(1,length(ebno));

for i=1:length(ebno)

%---Transmitter---------

%mapping of bits into symbols

symb=2.*data-1;

%----Filter

psf=ones(1,1);

M=length(psf);

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits);

%Passing the symbols from PSF

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebnos=10.^(ebno(i)/10);

n_var=1/sqrt(2.*ebnos);

rx_symb=tx_symb+n_var*randn(1,length(tx_symb));

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(M:M:length(rx_match));

rx=rx(1:1:bits);

recv_bits=(sign(rx)+1)./2;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with Rectangular Pulse Shaping for BPSK');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for BPSK')

legend('simulation','theory')

grid on

QPSK MATLAB code

clc

clear all

bits=1000000;

data=randint(1,bits)>0.5;

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:10;

BER=zeros(1,length(ebno));

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/2;

I=zeros(1,col);

Q=I;

I=data(1:2:bits-1);

Q=data(2:2:bits);

I= -2.*I+1;

Q= -2.*Q+1;

symb=I+j.*Q;

%----Filter

psf=ones(1,1);

%----

M=length(psf);

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/2);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/2);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

npsd=10.^(ebno(i)/10);

n_var=1/sqrt(2.*npsd);

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(M:M:length(rx_match));

rx=rx(1:1:bits/2);

recv_bits=zeros(1,bits);

%demapping

k=1;

for ii=1:bits/2

recv_bits(k)= -( sign( real( rx(ii) ) ) -1)/2;

recv_bits(k+1)=-( sign( imag( rx(ii) ) ) -1)/2;

k=k+2;

end

%sign( real( rx ) )

%sign( imag( rx ) )

%data

%tx_symb

%rx_symb

%recv_bits

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with Rectangular Pulse Shaping for QPSK');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for QPSK')

legend('Simulation','Theory')

grid on

8 QAM MATLAB CODE

clc

clear all

bits=3000000;

data=randint(1,bits)>0.5;

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:10;

BER=zeros(1,length(ebno));

thr=BER;

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/3;

I=zeros(1,col);

Q=I;

k=1;

for i=1:3:length(data)

if(data(i:i+2)==[0 0 0])

I(k)=1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 0 1])

I(k)=3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 0])

I(k)=-1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 1])

I(k)=-3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[1 0 0])

I(k)=1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 0 1])

I(k)=3;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 0])

I(k)=-1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 1])

I(k)=-3;

Q(k)=-1;

k=k+1;

end

symb=I+j*Q;

%real(symb)

%imag(symb)

%----Filter

psf=ones(1,1);

Es=sum(psf.^2);

eb=Es/3;

eb=2;

%----

M=length(psf);

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/3);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/3);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10.^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(M:M:length(rx_match));

rx=rx(1:1:bits/3);

recv_bits=zeros(1,bits);

%demapping

k=1;

for n=1:bits/3

I=real(rx(n));

Q=imag(rx(n));

if (I > 0) && (I < 2) && (Q > 0)

recv_bits(k:k+2)=[0 0 0];

elseif (I > 0) && (I < 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 0];

elseif (I > 2) && (Q >0)

recv_bits(k:k+2)=[0 0 1];

elseif (I > 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 1];

elseif (I < 0) && (I > -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 0];

elseif (I < 0) && (I > -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 0];

elseif (I < -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 1];

elseif (I < -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 1];

end

k=k+3;

end

tx_symb;

rx_symb;

data;

recv_bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

ebno_lin=(10^(ebno(i)/10))

thr(i)=(5/12)*erfc(sqrt(ebno_lin/2));

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with Rectangular Pulse Shaping for 8QAM');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

%ebno2=(10.^(ebno/10));

%thr=(5/12).*erfc(sqrt((10.^(ebno/10))./2));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for 8-QAM')

legend('Simulation','Theory')

grid on

BPSK With SQRC MATLAB code :

clc;

clear all;

bits=1000000;

data=randint(1,bits)>0.5;

ebno=0:11;

BER=zeros(1,length(ebno));

%---Transmitter---------

%mapping of bits into symbols

symb=2.*data-1;

%----Filter

interval=3;

T=4;

num_coff=2*interval*T+1

%num_coff=10;

hn=zeros(1,num_coff);

beta=0.2;

PI=22/7;

k=1;

for n=-interval : 1/T : interval

if(n==0)

hn(k)=1-beta+4*beta/PI;

elseif( n==1/(4*beta) || n==-1/(4*beta) )

hn(k)=beta*cos( 0.25*PI*(1-1/beta) ) - (2*beta/PI)* cos( 0.25*PI*(1+1/beta) );

else

hn(k)=( sin(PI*n*(1-beta)) + 4*beta*n*cos(PI*n*(1+beta)) )/(PI*n*(1-16*beta^2*n^2));

end

k=k+1;

end

n=-interval : 1/T : interval ;

%hn=ones(1,1)

psf=hn(1:1:length(n));

psf=psf/sqrt(sum(psf.^2));

%psf=ones(1,1);

figure

stem(n,psf)

%xxxxxxxx

%Energy of bit

Es=sum(psf.^2);

eb=Es;

%xxxxxxxxxxxxxxxxxxx

%M=length(psf);

M=4;

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits);

%Passing the symbols from PSF

tx_symb=conv(upsamp2,psf);

%tx_symb=tx_symb(1:length(upsamp2));

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)));

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(num_coff:T:length(rx_match)-num_coff);

rx=rx(1:1:bits);

recv_bits=(sign(rx)+1)./2;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with SQRC Pulse Shaping for BPSK');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

data;

upsamp2;

recv_bits;

%stem(tx_symb)

figure

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate of BPSK With SQRC')

legend('Simulation','Theory')

grid on

QPSK With SQRC MATLAB code:

clc

clear all

bits=1000000;

data=randint(1,bits)>0.5;

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:11;

BER=zeros(1,length(ebno));

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/2;

I=zeros(1,col);

Q=I;

I=data(1:2:bits-1);

Q=data(2:2:bits);

I= -2.*I+1;

Q= -2.*Q+1;

symb=I+j.*Q;

%----Filter

interval=3;

T=4;

num_coff=2*interval*T+1

%num_coff=1;

hn=zeros(1,num_coff);

beta=0.2;

PI=22/7;

k=1;

for n=-interval : 1/T : interval

if(n==0)

hn(k)=1-beta+4*beta/PI;

elseif( n==1/(4*beta) || n==-1/(4*beta) )

hn(k)=beta*cos( 0.25*PI*(1-1/beta) ) - (2*beta/PI)* cos( 0.25*PI*(1+1/beta) );

else

hn(k)=( sin(PI*n*(1-beta)) + 4*beta*n*cos(PI*n*(1+beta)) )/(PI*n*(1-16*beta^2*n^2));

end

k=k+1;

end

n=-interval : 1/T : interval ;

%hn=ones(1,1)

psf=hn(1:1:length(n));

psf=psf/sqrt(sum(psf.^2));

%psf=ones(1,1);

figure

% stem(n,psf)

%xxxxxxxx

%Energy of bit

Es=sum(psf.^2);

eb=Es;

%----

M=4;

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/2);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/2);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(num_coff:T:length(rx_match)-num_coff);

%rx=rx(1:1:bits/2);

recv_bits=zeros(1,bits);

%demapping

k=1;

for ii=1:bits/2

recv_bits(k)= -( sign( real( rx(ii) ) ) -1)/2;

recv_bits(k+1)=-( sign( imag( rx(ii) ) ) -1)/2;

k=k+2;

end

%sign( real( rx ) )

%sign( imag( rx ) )

%data

%tx_symb

%rx_symb

%recv_bits

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with SQRC Pulse Shaping for QPSK');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for QPSK with SQRC')

legend('simulation','theory')

grid on

8 QAM With SQRC MATLAB code

clc

clear all

bits=3000000;

data=randint(1,bits)>0.5;

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:.5:14.5;

BER=zeros(1,length(ebno));

thr=BER;

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/3;

I=zeros(1,col);

Q=I;

k=1;

for i=1:3:length(data)

if(data(i:i+2)==[0 0 0])

I(k)=1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 0 1])

I(k)=3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 0])

I(k)=-1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 1])

I(k)=-3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[1 0 0])

I(k)=1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 0 1])

I(k)=3;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 0])

I(k)=-1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 1])

I(k)=-3;

Q(k)=-1;

k=k+1;

end

symb=I+j*Q;

%real(symb)

%imag(symb)

%----Filter

interval=3;

T=4;

num_coff=2*interval*T+1

%num_coff=1;

hn=zeros(1,num_coff);

beta=0.2;

PI=22/7;

k=1;

for n=-interval : 1/T : interval

if(n==0)

hn(k)=1-beta+4*beta/PI;

elseif( n==1/(4*beta) || n==-1/(4*beta) )

hn(k)=beta*cos( 0.25*PI*(1-1/beta) ) - (2*beta/PI)* cos( 0.25*PI*(1+1/beta) );

else

hn(k)=( sin(PI*n*(1-beta)) + 4*beta*n*cos(PI*n*(1+beta)) )/(PI*n*(1-16*beta^2*n^2));

end

k=k+1;

end

n=-interval : 1/T : interval ;

%hn=ones(1,1)

psf=hn(1:1:length(n));

%psf=ones(1,1);

psf=psf./sqrt((sum(psf.^2)));

Es=sum(psf.^2);

eb=Es;

%we need to remove this

eb=2;

%xxxxxxxxxxxxxxx

%----

M=4;

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/3);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/3);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10.^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(num_coff:T:length(rx_match)-num_coff);

%rx=rx(1:1:bits/3);

recv_bits=zeros(1,bits);

%demapping

k=1;

for n=1:bits/3

I=real(rx(n));

Q=imag(rx(n));

if (I > 0) && (I < 2) && (Q > 0)

recv_bits(k:k+2)=[0 0 0];

elseif (I > 0) && (I < 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 0];

elseif (I > 2) && (Q >0)

recv_bits(k:k+2)=[0 0 1];

elseif (I > 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 1];

elseif (I < 0) && (I > -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 0];

elseif (I < 0) && (I > -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 0];

elseif (I < -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 1];

elseif (I < -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 1];

end

k=k+3;

end

tx_symb;

rx_symb;

data;

recv_bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(recv_bits,data));

errors=size(errors,2);

BER(i)=errors/bits;

ebno_lin=(10^(ebno(i)/10))

thr(i)=(5/12)*erfc(sqrt(ebno_lin/2));

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal with SQRC Pulse Shaping for 8QAM');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

%ebno2=(10.^(ebno/10));

%thr=(5/12).*erfc(sqrt((10.^(ebno/10))./2));

semilogy(ebno,thr,'rx-');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for 8-QAM with SQRC')

legend('simulation','theory')

grid on

BPSK Coded matlab code

clc;

clear all;

bits=4000000;

gen_data=randint(1,bits)>0.5;

uncoded_data = gen_data;

bits=bits*7/4;

%coding

n=7;

k=4;

P=[0 1 1;1 0 1;1 1 0;1 1 1];

G=[P eye(4)];

H=[eye(n-k) P.'];

Ht=H.';

e=[zeros(1,7);diag(ones(1,7))];

synd_table=[ mod(e*Ht,2) e];

U=zeros(1,length(gen_data)*7/4);

kk=1;

for ii=1:4:length(gen_data)

U(kk:kk+6)=mod(gen_data(ii:ii+3)*G,2);

kk=kk+7;

end

%xxxxxxxx

%coded data

data=U;

%xxxxx

ebno=0:10;

BER=zeros(1,length(ebno));

for i=1:length(ebno)

%---Transmitter---------

%mapping of bits into symbols

symb=2.*data-1;

%----Filter

psf=ones(1,1);

M=length(psf);

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits);

%Passing the symbols from PSF

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

eb=1.6;

ebno2=10.^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+ n_var*randn(1,length(tx_symb)) ;

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(M:M:length(rx_match));

rx=rx(1:1:bits);

recv_bits=(sign(rx)+1)./2;

recvd_coded_bits=recv_bits;

%decoding

corrected_coded_bits=zeros(1,length(recvd_coded_bits));

uncoded_bits=zeros(1,length(gen_data));

length(gen_data)

c=1;

for kkk=1:7:length(recvd_coded_bits)

S=mod(recvd_coded_bits(kkk:kkk+6)*Ht,2);

for iii=1:8

if S==[synd_table(iii,1) synd_table(iii,2) synd_table(iii,3)]

ed=[synd_table(iii,4) synd_table(iii,5) synd_table(iii,6) ...

synd_table(iii,7) synd_table(iii,8) synd_table(iii,9) ...

synd_table(iii,10) ];

end

corrected_coded_bits(kkk:kkk+6)=xor(recvd_coded_bits(kkk:kkk+6),ed);

uncoded_bits(c:c+3)=corrected_coded_bits(kkk+3:kkk+6);

c=c+4;

end

corrected_coded_bits;

uncoded_bits;

length(uncoded_bits);

length(gen_data);

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

%---SIMULATED BIT ERROR RATE----

errors=find(xor(uncoded_bits,gen_data));

errors=size(errors,2);

BER(i)=errors/length(gen_data);

Pc(i)=0.5*erfc(sqrt((4/7)*10.^(ebno(i)/10)));

PC2(i)=0;

for ii=2:7

PC2(i)=PC2(i)+ii*nchoosek(7,ii)*Pc(i)^ii*(1-Pc(i))^(7-ii);

end

Pb_th(i)=PC2(i)/7;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal for Coded BPSK with SQRC');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

uncoded_data;

ed;

corrected_coded_bits;

uncoded_bits;

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

hold on

semilogy(ebno,Pb_th,'-ok');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate for Coded BPSK')

legend('Simulation','Theory Uncoded','Theory Coded')

grid on

QPSK with coded matlab code:

clc

clear all

bits=4000000;

gen_data=randint(1,bits)>0.5;

uncoded_data = gen_data;

bits=bits*7/4;

%coding

n=7;

k=4;

P=[0 1 1;1 0 1;1 1 0;1 1 1];

G=[P eye(4)];

H=[eye(n-k) P.'];

Ht=H.';

e=[zeros(1,7);diag(ones(1,7))];

synd_table=[ mod(e*Ht,2) e];

U=zeros(1,length(gen_data)*7/4);

kk=1;

for ii=1:4:length(gen_data)

U(kk:kk+6)=mod(gen_data(ii:ii+3)*G,2);

kk=kk+7;

end

%xxxxxxxx

%coded data

data=U;

%xxxxx

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:10;

BER=zeros(1,length(ebno));

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/2;

I=zeros(1,col);

Q=I;

I=data(1:2:bits-1);

Q=data(2:2:bits);

I= -2.*I+1;

Q= -2.*Q+1;

symb=I+j.*Q;

%----Filter

interval=3;

T=4;

num_coff=2*interval*T+1

%num_coff=1;

hn=zeros(1,num_coff);

beta=0.2;

PI=22/7;

k=1;

for n=-interval : 1/T : interval

if(n==0)

hn(k)=1-beta+4*beta/PI;

elseif( n==1/(4*beta) || n==-1/(4*beta) )

hn(k)=beta*cos( 0.25*PI*(1-1/beta) ) - (2*beta/PI)* cos( 0.25*PI*(1+1/beta) );

else

hn(k)=( sin(PI*n*(1-beta)) + 4*beta*n*cos(PI*n*(1+beta)) )/(PI*n*(1-16*beta^2*n^2));

end

k=k+1;

end

n=-interval : 1/T : interval ;

%hn=ones(1,1)

psf=hn(1:1:length(n));

psf=psf/sqrt(sum(psf.^2));

%psf=ones(1,1);

figure

% stem(n,psf)

%xxxxxxxx

%Energy of bit

Es=sum(psf.^2);

eb=Es;

eb=1.55

%----

M=4;

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/2);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/2);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(num_coff:T:length(rx_match)-num_coff);

%rx=rx(1:1:bits/2);

recv_bits=zeros(1,bits);

%demapping

k=1;

for ii=1:bits/2

recv_bits(k)= -( sign( real( rx(ii) ) ) -1)/2;

recv_bits(k+1)=-( sign( imag( rx(ii) ) ) -1)/2;

k=k+2;

end

recvd_coded_bits=recv_bits;

%decoding

corrected_coded_bits=zeros(1,length(recvd_coded_bits));

uncoded_bits=zeros(1,length(gen_data));

length(gen_data)

c=1;

for kkk=1:7:length(recvd_coded_bits)

S=mod(recvd_coded_bits(kkk:kkk+6)*Ht,2);

for iii=1:8

if S==[synd_table(iii,1) synd_table(iii,2) synd_table(iii,3)]

ed=[synd_table(iii,4) synd_table(iii,5) synd_table(iii,6) ...

synd_table(iii,7) synd_table(iii,8) synd_table(iii,9) ...

synd_table(iii,10) ];

end

corrected_coded_bits(kkk:kkk+6)=xor(recvd_coded_bits(kkk:kkk+6),ed);

uncoded_bits(c:c+3)=corrected_coded_bits(kkk+3:kkk+6);

c=c+4;

end

corrected_coded_bits;

uncoded_bits;

length(uncoded_bits);

length(gen_data);

%---SIMULATED BIT ERROR RATE----

errors=find(xor(uncoded_bits,gen_data));

errors=size(errors,2);

BER(i)=errors/length(gen_data);

Pc(i)=0.5*erfc(sqrt((4/7)*10.^(ebno(i)/10)));

PC2(i)=0;

for ii=2:7

PC2(i)=PC2(i)+ii*nchoosek(7,ii)*Pc(i)^ii*(1-Pc(i))^(7-ii);

end

Pb_th(i)=PC2(i)/7;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal for Coded QPSK with SQRC');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

thr=0.5*erfc(sqrt(10.^(ebno/10)));

semilogy(ebno,thr,'rx-');

hold on

semilogy(ebno,Pb_th,'-ok');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate (Coded QPSK)')

legend('Simulation','Theory Uncoded','Theory Coded')

grid on

8 QAM Coded matlab code:

clc

clear all

bits=3000000;

gen_data=randint(1,bits)>0.5;

uncoded_data = gen_data;

bits=bits*7/4;

%coding

n=7;

k=4;

P=[0 1 1;1 0 1;1 1 0;1 1 1];

G=[P eye(4)];

H=[eye(n-k) P.'];

Ht=H.';

e=[zeros(1,7);diag(ones(1,7))];

synd_table=[ mod(e*Ht,2) e];

U=zeros(1,length(gen_data)*7/4);

kk=1;

for ii=1:4:length(gen_data)

U(kk:kk+6)=mod(gen_data(ii:ii+3)*G,2);

kk=kk+7;

end

%xxxxxxxx

%coded data

data=U;

%xxxxx

%---debugging---

%data=[1 1 1]

%xxxxxxxxxx

ebno=0:14;

BER=zeros(1,length(ebno));

thr=BER;

%---Transmitter---------

%Gray mapping of bits into symbols

col=length(data)/3;

I=zeros(1,col);

Q=I;

k=1;

for i=1:3:length(data)

if(data(i:i+2)==[0 0 0])

I(k)=1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 0 1])

I(k)=3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 0])

I(k)=-1;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[0 1 1])

I(k)=-3;

Q(k)=1;

k=k+1;

elseif(data(i:i+2)==[1 0 0])

I(k)=1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 0 1])

I(k)=3;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 0])

I(k)=-1;

Q(k)=-1;

k=k+1;

elseif(data(i:i+2)==[1 1 1])

I(k)=-3;

Q(k)=-1;

k=k+1;

end

symb=I+j*Q;

%real(symb)

%imag(symb)

%----Filter

interval=3;

T=4;

num_coff=2*interval*T+1

%num_coff=1;

hn=zeros(1,num_coff);

beta=0.2;

PI=22/7;

k=1;

for n=-interval : 1/T : interval

if(n==0)

hn(k)=1-beta+4*beta/PI;

elseif( n==1/(4*beta) || n==-1/(4*beta) )

hn(k)=beta*cos( 0.25*PI*(1-1/beta) ) - (2*beta/PI)* cos( 0.25*PI*(1+1/beta) );

else

hn(k)=( sin(PI*n*(1-beta)) + 4*beta*n*cos(PI*n*(1+beta)) )/(PI*n*(1-16*beta^2*n^2));

end

k=k+1;

end

n=-interval : 1/T : interval ;

%hn=ones(1,1)

psf=hn(1:1:length(n));

%psf=ones(1,1);

psf=psf./sqrt((sum(psf.^2)));

Es=sum(psf.^2);

eb=Es;

%we need to remove this

eb=2.9;

%xxxxxxxxxxxxxxx

%----

M=4;

for i=1:length(ebno)

% inserting zeros between the bits

% w.r.t number of coefficients of

% PSF to pass the bit stream from the PSF

z=zeros(M-1,bits/3);

upsamp=[symb;z];

upsamp2=reshape(upsamp,1,(M)*bits/3);

%Passing the symbols from PSF

%tx_symb=conv(real(upsamp2),psf)+j*conv(imag(upsamp2),psf);

tx_symb=conv(upsamp2,psf);

%--------CHANNEL-----------

%Random noise generation and addition to the signal

ebno2=10.^(ebno(i)/10);

%no=eb/ebno2;

%n_var=sqrt(no/2);

n_var=sqrt(eb/(2*ebno2));

rx_symb=tx_symb+(n_var*randn(1,length(tx_symb)) +j*n_var*randn(1,length(tx_symb)) );

%xxxxxxxxxxxxxxxxxxxxxxxxxx

%-------RECEIVER-----------

rx_match=conv(rx_symb,psf);

rx=rx_match(num_coff:T:length(rx_match)-num_coff);

%rx=rx(1:1:bits/3);

recv_bits=zeros(1,bits);

%demapping

k=1;

for n=1:bits/3

I=real(rx(n));

Q=imag(rx(n));

if (I > 0) && (I < 2) && (Q > 0)

recv_bits(k:k+2)=[0 0 0];

elseif (I > 0) && (I < 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 0];

elseif (I > 2) && (Q >0)

recv_bits(k:k+2)=[0 0 1];

elseif (I > 2) && (Q < 0)

recv_bits(k:k+2)=[1 0 1];

elseif (I < 0) && (I > -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 0];

elseif (I < 0) && (I > -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 0];

elseif (I < -2) && (Q > 0)

recv_bits(k:k+2)=[0 1 1];

elseif (I < -2) && (Q < 0)

recv_bits(k:k+2)=[1 1 1];

end

k=k+3;

end

tx_symb;

rx_symb;

data;

recv_bits;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

recvd_coded_bits=recv_bits;

%decoded matlab code

corrected_coded_bits=zeros(1,length(recvd_coded_bits));

uncoded_bits=zeros(1,length(gen_data));

length(gen_data)

c=1;

for kkk=1:7:length(recvd_coded_bits)

S=mod(recvd_coded_bits(kkk:kkk+6)*Ht,2);

for iii=1:8

if S==[synd_table(iii,1) synd_table(iii,2) synd_table(iii,3)]

ed=[synd_table(iii,4) synd_table(iii,5) synd_table(iii,6) ...

synd_table(iii,7) synd_table(iii,8) synd_table(iii,9) ...

synd_table(iii,10) ];

end

corrected_coded_bits(kkk:kkk+6)=xor(recvd_coded_bits(kkk:kkk+6),ed);

uncoded_bits(c:c+3)=corrected_coded_bits(kkk+3:kkk+6);

c=c+4;

end

corrected_coded_bits;

uncoded_bits;

length(uncoded_bits);

length(gen_data);

%---SIMULATED BIT ERROR RATE----

errors=find(xor(uncoded_bits,gen_data));

errors=size(errors,2);

BER(i)=errors/length(gen_data);

ebno_lin=(10^(ebno(i)/10))

thr(i)=(5/12)*erfc(sqrt(ebno_lin/2));

Pc(i)=(5/12)*erfc(sqrt((4/14)*10.^(ebno(i)/10)));

PC2(i)=0;

for ii=2:7

PC2(i)=PC2(i)+ii*nchoosek(7,ii)*Pc(i)^ii*(1-Pc(i))^(7-ii);

end

Pb_th(i)=PC2(i)/7;

%xxxxxxxxxxxxxxxxxxxxxxxxxxx

end

fs=1;

n_pt=2^9;

tx_spec=fft(tx_symb,n_pt);

f= -fs/2:fs/n_pt:fs/2-fs/n_pt;

figure

plot(f,abs(fftshift(tx_spec)));

title('Signal Spectrum for Signal for Coded 8-QAM with SQRC');

xlabel('Frequency [Hz]');

ylabel('x(F)');

figure

semilogy(ebno,BER,'b.-');

hold on

%ebno2=(10.^(ebno/10));

%thr=(5/12).*erfc(sqrt((10.^(ebno/10))./2));

semilogy(ebno,thr,'rx-');

hold on

semilogy(ebno,Pb_th,'-ok');

xlabel('Eb/No (dB)')

ylabel('Bit Error rate')

title('Simulated Vs Theoritical Bit Error Rate of Coded 8QAM')

legend('simulation','Theory Uncoded','Theory Coded')

grid on